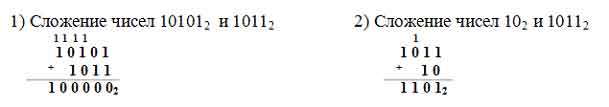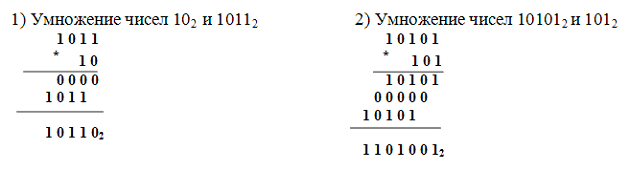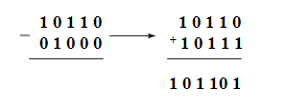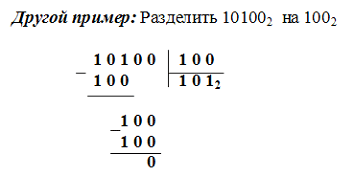Кодирование информации без компьютеров
Системы кодирования числовой информации
Двоичная система счисления
Перевод чисел из одной системы счисления в другую
Кодирование информации на компьютере
Вопросы и упражнения
Двоичная система счисления
Вопреки распространённому заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, ещё в 17 веке. Великий немецкий учёный Лейбниц считал:
«Вычисление с помощью двоек... является для науки основным и порождает новые открытия... При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок».
Впервые двоичная система появилась в 1605 году в работах Томаса Хэрриота (он изобрёл знаки > и <). Позже двоичная система была забыта, и только в 1936-1938 гг. американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
Двоичная система удобна для компьютера, но неудобна для человека - числа получаются очень длинными и их трудно записывать и запоминать. Она используется, как правило, для «внутренних нужд» компьютера. Двоичная система счисления позволяет достаточно просто организовать числа, и для того, чтобы представить число в ЭВМ, достаточно иметь устройство, которое обладает только двумя устойчивыми состояниями, одно из которых соответствует логической «1», а другое - «0». Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. Для десятичной системы счисления понадобилось бы, к примеру, устройство с 10 устойчивыми состояниями. Это значительно усложнило бы схему ЭВМ.
Другим важным достоинством двоичной системы является простота вычислений. Рассмотрим, как выполняются арифметические действия в двоичной системе. Для этого проведём анализ таблиц сложения и умножения в двоичной системе.

Примеры сложения двоичных чисел:
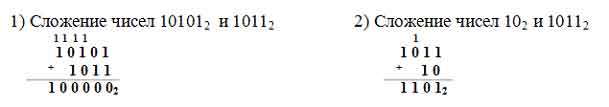
Примеры умножения двоичных чисел:
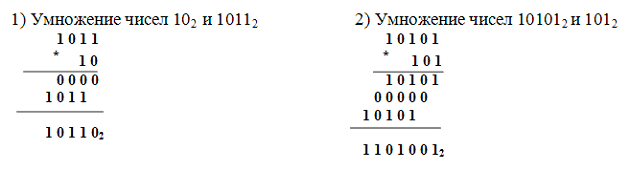
Следует обратить внимание на аналогию в правилах выполнения арифметических действий в двоичной и десятичной системах счисления: например, если при сложении двух двоичных чисел сумма цифр окажется больше единицы, то возникает перенос в старший разряд.
Вычитание двоичных чисел осуществляется следующим образом: Вычитаемое число преобразуется в дополнительный код. Например, если надо вычесть из числа 10110 число 01000, то вычитаемое 01000 преобразуется в дополнительный код так: в числе вместо 0 пишется 1, а вместо 1 пишется 0, следовательно, получим из вычитаемого число 10111. Затем преобразованное число складывается с уменьшаемым:
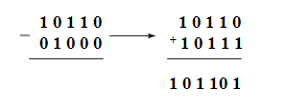
И вычитаемое, и уменьшаемое состоят из 5 разрядов, а результат суммы - число 6-разрядное. Старший разряд суммы отнимается от числа и складывается с результатом:


Такой приём часто используется в практике вычислений. Например, в десятичной системе числа можно вычесть так. Допустим требуется найти разность 842-623. Представим число 623 в дополнительный вид, отняв его от 1000. Получим число 377. Затем найдём сумму: 842+377=1219. Отбросим перенос в старший разряд и получим число 219. Мы нашли решение этого примера.

Деление двоичных чисел выполняется аналогично делению десятичных чисел. Вычитание и умножение в процессе деления необходимо выполнять рассмотренными ранее способами.
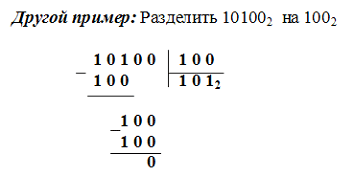
Важнейшее преимущество двоичной арифметики заключается в том, что она позволяет все арифметические действия свести к одному - сложению, а это значительно упрощает устройство процессора ЭВМ. Отметим недостаток, характерный для двоичной системы счисления - значительный рост числа разрядов при увеличении числа. Но все достоинства этой системы делают такой недостаток не столь существенным.

|

|